Learn About the Important Theorem – Pythagorean Theorem

In mathematical studies, the Pythagorean theorem is a vital concept that is required to be grasped by the student. Studying this theorem is very much helpful for the students.

Many important concepts are being covered in this section. Well, a Pythagoras theorem denotes the relationship between the sides of a right-angle triangle.

With the help of the Pythagoras Theorem the hypotenuse, base, and perpendicular of the right-angled triangle can be estimated. 

Pythagoras Theorem Explained in the Form of a Statement

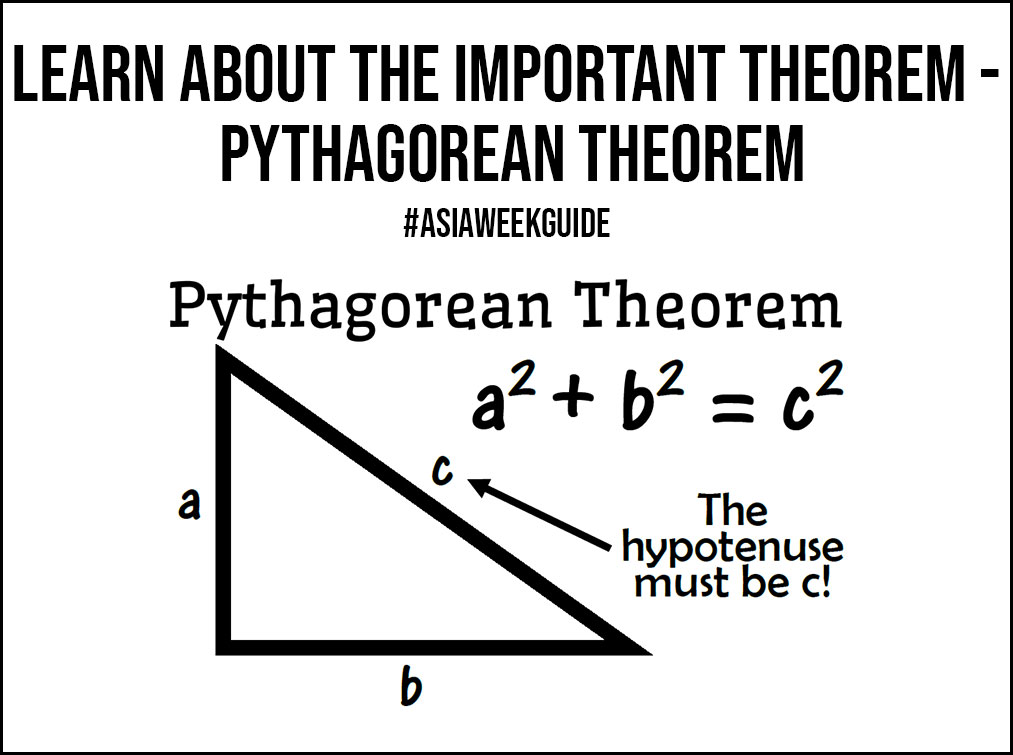
The Pythagoras Theorem states that “considering that a triangle is a right-angled triangle, the square of the hypotenuse side will be exactly equal to the summation of squares of the remaining two sides of that right-angled triangle”.

While, this is to be noted that, the sides of the right-angled triangle is known as the:

• Perpendicular
• Base
• Hypotenuse

In a right-angled triangle, the hypotenuse side is the longest side. The hypotenuse has the longest measurement as the opposite angle is always 90 degrees.

Also Read: What is EPFO Exam in India? Eligibility, Syllabus, Age Limit, Fees, Registration

Pythagoras Theorem is Credited to Whom?

Pythagoras Theorem is named after a Greek Mathematician who was named as ‘Pythagoras’, from his name the theorem is honored.

Lay Out the Formula of The Pythagoras Theorem

In order to understand the formula better, let us consider a right-angled triangle that has three sides namely – R T Y

R is the Perpendicular side, T is the Base, while Y is the Hypotenuse.

With this consideration, we can draft the Pythagoras Theorem which is as follows:

Y² = R² + T² 

This formula is based on the formula – Hypotenuse² = Perpendicular² + Base²

Example Of a Pythagoras Theorem

An example will make the understanding much clearer. Let us consider there is a right-angled triangle whose Hypotenuse side is unknown, while the base and Perpendicular is 4 and 3 respectively. You need to find out the value of the hypotenuse side.

Solution: Let us consider the value of the Hypotenuse side to be ‘x’.

With the help of the theorem, we can find out the value of the x that is the Hypotenuse side.

Hypotenuse² = Base² + Perpendicular²

X² = 4² + 3²

X^{2 =} 16 + 9

X² = 25

X = √25

X = 5

Thus, the value of X or the Hypotenuse side is 5.

What Is an Isosceles Triangle?

An isosceles triangle is the one where any of the two sides have an equal measurement of length.

Also, the angles which are placed opposite two equal sides measure the equal angle. Thus, the triangles have three sides which are based on the measurement, they are:

• Scalene Triangle
• Isosceles Triangle
• Equilateral Triangle

Now we will learn about the Isosceles Triangle.

Define Isosceles Triangle

If two of the sides of the triangle are equal in measurement, that triangle is called an isosceles triangle.

Even the two angles given opposite to the two equal sides of the isosceles triangle are equal too. Thus, it means – an isosceles triangle is one that has two of its sides congruent in nature.

Example: There is a triangle named QPR, in this Triangle, PQ and QR have equal sides, then this is known as the isosceles triangle.

Also, the angles supposed named as angle G and Angle O will have an equal degree of inclination.

Also Read: Top 26 Subject-verb Agreement Rules

Chalk out the Properties of Isosceles Triangle

The properties of the Isosceles Triangle are numbered down as follows:

• The two sides of the isosceles triangle are equal in measurement.
• The side which is unequal is actually the base of the triangle.
• The angles which are placed opposite to the equal sides are also equal in measurement.
• In order to measure the height or altitude of the isosceles triangle, then it is to be measured from the vase to the vertex of the isosceles triangle.
• While the third angle will always be 90 degrees of a right isosceles triangle.

Visit Cuemath to learn more amazing concepts.